GSTDECOMP - Eigen decomposition of a tensor field.

Contents

Description

Perform the eigen decomposition of a (symmetric) tensor field given by its entries, or the reconstruction of a tensor field given by its eigen- decomposition and/or orientation.

Syntax

     [l1,l2] = GSTDECOMP(gx2, gy2, gxy);
     [l1,l2,e1,e2] = GSTDECOMP(gx2, gy2, gxy);
     [l1,l2,e1,e2,theta] = GSTDECOMP(gx2, gy2, gxy, dblangle);
     [l1,l2,e1,e2] = GSTDECOMP(T);
     [l1,l2,e1,e2,theta] = GSTDECOMP(T, dblangle);
     [gx2, gy2, gxy] = GSTDECOMP(l1,l2,e1,e2);
     T = GSTDECOMP(l1,l2,e1,e2);
     [gx2, gy2, gxy] = GSTDECOMP(l1,l2,theta);
     T = GSTDECOMP(T, theta);

Remarks

See Kroon's derivatives library and Koethe's VIGRA library; avaialble at http://hci.iwr.uni-heidelberg.de/vigra/doc/vigra/group__TensorImaging.html, http://hci.iwr.uni-heidelberg.de/vigra/doc/vigra/tensorutilities_8hxx-source.html.

See also

Ressembles: GSTSMOOTH, EIGENDECOMP2X2SYM.

Function implementation

function [out,varargout] = gstdecomp(in, varargin)

parsing parameters

error(nargchk(1, 4, nargin, 'struct'));
error(nargoutchk(1, 5, nargout, 'struct'));

calculation

if (nargout==1 && nargin>1) || nargout==3

    switch nargin
        case 2 % new tensor from tensor entries and orientation
            [l1,l2] = gstdecomp(in);
            [gx2, gy2, gxy] = gstrecomp(l1, l2, varargin{1});

        case 3 % new tensor from eigenvalues and orientation
            l1 = in; l2 = varargin{1};
            [gx2, gy2, gxy] = gstrecomp(l1, l2, varargin{2});

        case 4 % tensor entries from eigen decomposition
            l1 = in;     l2 = varargin{1};
            [gx2, gy2, gxy] = gstrecomp(l1, l2, varargin{2}, varargin{3});
    end

    switch nargout
        case 1
            out(:,:,1,1) = gx2;
            out(:,:,2,2) = gy2;
            out(:,:,1,2) = gxy;
            out(:,:,2,1) = out(:,:,1,2);

        case 3
            out = gx2;
            varargout{1} = gy2;
            varargout{2} = gxy;
    end

elseif (nargin==1&&nargout==1) || nargout==2 || nargout>=4

    dbleangle = false;

    % tensor entries
    switch nargin
        case {1,2} % the tensor has been passed
            gy2 = in(:,:,2,2);
            gxy = in(:,:,1,2);
            gx2 = in(:,:,1,1);
            if nargin==2, dbleangle = varargin{1};  end

        case {3,4}
            gx2 = in;
            gy2 = varargin{1};
            gxy = varargin{2};
            if nargin==4, dbleangle = varargin{3};  end
    end

    % set the method used for estimating the eigenvectors
    if dbleangle,   method = 'koe';  % 'kro'
    else            method = 'pey';
    end

(i) compute the eigenvalues

    if any(strcmpi(method,{'koe','kro'}))
        % VIGRA expression: see file tensorutilities.hxx, function
        % tensorEigenRepresentation
        % Kroon expression: see file EigenVectors2D.m
        d1 = gx2 + gy2; %src.getComponent(s,0) + src.getComponent(s,2);
        d2 = gx2 - gy2; %src.getComponent(s,0) - src.getComponent(s,2);
        d3 = 2 * gxy;   %2.0 * src.getComponent(s,1);
        d4 = sqrt(d2.^2 + d3.^2); % hypot(d2, d3)
        % root = d4;
        l1 = 0.5 * (d1+d4); %dest.setComponent(0.5 * (d1 + d4), d, 0);
        l2 = 0.5 * (d1-d4); %dest.setComponent(0.5 * (d1 - d4), d, 1);

    elseif strcmpi(method,'pey')
        % another expression for eigenvalues
        t = 0.5 * (gx2+gy2);     % trace/2
        a = gx2 - t;  % a = 0.5 * (gx2-gy2);
        ab2 = sqrt(a.^2 + gxy.^2); % we have root = 2 * ab2; (see above)
        l1 = t + ab2;
        l2 = t - ab2;

    end

    out = l1;
    varargout{1} = l2;

(ii) compute the eigenvectors

    if nargout>2

        if strcmpi(method,'koe')
            % double angle representation: theta in [-pi/2,pi/2]
            %    %theta = gstfeature(gx2, gy2, gxy, 'orient');
            theta = 0.5 * atan2(d3, d2);
            %dest.setComponent(0.5 * VIGRA_CSTD::atan2(d3, d2), d, 2);
            % note: atan2(0,0)=0
            % principal eigen vector
            e1(:,:,1) = cos(theta);
            e1(:,:,2) = sin(theta);

        elseif strcmpi(method,'pey')
            % atan2 expression for orientation: atan2(l1-gx2,gxy)
            theta = atan2( ab2-a, gxy );
            e1(:,:,1) = cos(theta);
            e1(:,:,2) = sin(theta);

        elseif strcmpi(method,'kro')
            % note: no theta computed here
            vx = d3;
            vy = d4 - d2;
            mag = sqrt(vx.^2 + vy.^2);
            i = (mag ~= 0);
            vx(i) = vx(i)./mag(i);
            vy(i) = vy(i)./mag(i);

            e1(:,:,1) = vx;
            e1(:,:,2) = vy;
        end

        %  eigenvectors are orthogonal
        e2(:,:,1) = -e1(:,:,2);
        e2(:,:,2) = e1(:,:,1);

        varargout{2} = e1;
        varargout{3} = e2;
        if nargout==5, varargout{4} = theta;  end

    end

end

end % end of gstdecomp

Subfunction

GSTRECOMP - Compute the entries of the (symmetric) tensor field which corresponds to the given eigendecomposition.

e1(i,j,:) is the main eigenvector at location (i,j) with associated largest eigenvalue l1(i,j). e2(i,j,:) is the second eigenvector at location (i,j) with associated smallest eigenvalue l2(i,j).

Regarding the GST, we have: 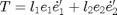$T = l_1 e_1 \dot e_1' + l_2 e_2 \dot e_2'$

%--------------------------------------------------------------------------
function [gx2, gy2, gxy] = gstrecomp(l1,l2,e1,varargin)

switch nargin
    case 3
        % then the orientation has been passed
        theta = e1;
        e1(:,:,1) = cos(theta);
        e1(:,:,2) = sin(theta);
        e2(:,:,1) = -e1(:,:,2);
        e2(:,:,2) = e1(:,:,1);

    case 4
        % both eigenvectors have been passed
        e2 = varargin{1};
end

gx2 = l1.*e1(:,:,1).^2 + l2.*e2(:,:,1).^2;
gxy = l1.*e1(:,:,1).*e1(:,:,2) + l2.*e2(:,:,1).*e2(:,:,2);
gy2 = l1.*e1(:,:,2).^2 + l2.*e2(:,:,2).^2;
end