BILATERAL_BASE - Base function for standard Gaussian bilateral filter.

Contents

Description

Perform bilateral filtering on monochrome images following the approach of [TM98]. Both the domain and range filters are Gaussian filters.

Algorithm

The bilateral filter is a spatially varying filter that better preserves edges than the Gaussian filter.

Given a spacial width 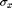$\sigma_x$ and a range width $\sigma_r$, the filter opterates as:

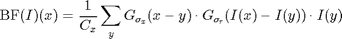
$$ \mbox{BF}(I)(x) = \frac{1}{C_x} \sum_y G_{\sigma_x}(x-y) \cdot G_{\sigma_r}(I(x)-I(y)) \cdot I(y) $$

with the normalization factor:

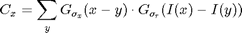
$$ C_x = \sum_y G_{\sigma_x}(x-y) \cdot G_{\sigma_r}(I(x)-I(y))$$

at a given pixel x, it corresponds to an averaring with the data-dependant kernel 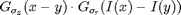$G_{\sigma_x}(x-y) \cdot G_{\sigma_r}(I(x)-I(y))$.

Syntax

    F = BILATERAL_BASE(I, sigma_d, sigma_r);

Inputs

I : input image, possibly multispectral.

sigma_d : standard deviation of domain filter (in pixels); sub-pixel values quantized to even fractions, i.e. in steps of 0.2.

sigma_r : standard deviation of range filter; value in range [0,1] (relative to colorspace range which is normalized to 0 - 1).

Output

F : filtered image.

Reference

[TM98] C. Tomasi and R. Manduchi: "Bilateral filtering for gray and color images", Proc. IEEE ICCV, 1998. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=710815&tag=1

See also

Ressembles: BILATERAL, BILATERALSTACK_BASE. Requires: GAUSSWIN.

Function implementation

function  F = bilateral_base(I, sigma_d, sigma_r)

[X,Y,C] = size(I);

deal with multispectral images

if C>1
    F = I;
    for i=1:C
        F(:,:,i) = bilateral_base(I(:,:,i), sigma_d, sigma_r);
    end
    return
end

main computation

I = rescale(I);   % normalize image range to 0 - 1
F = I; % initialize output;

initialize domain filter kernel

d_filter = gausswin(5*sigma_d);  % see "doc gausswin" for details
filtlength = length(d_filter);   % filter length determined by domain
if filtlength == 0
    F = I;
    return;
end
d_filter = d_filter*d_filter';  % 2D filter

initialize range filter

if sigma_r == 0
    sigma_r = eps;
end
mu_r = I;       % Extract means for range filter
I = padarray(I, floor(filtlength/2)*[1,1]);    % zero-padding for filtering
k = zeros(size(F));     % Initialize normalizing factor

filter using sliding window and accumulate (more efficient than px by px)

for a = 1:filtlength
    for b = 1:filtlength
        win = I(a:a+Y-1,b:b+X-1);    % sliding window
        r_coeffs = exp(-((win-mu_r).^2)./(2*sigma_r^2));  % range filter coefficients
        d_coeff = d_filter(a,b);    % domain filter coefficient
        F = F + d_coeff*r_coeffs.*win;  % accumulate
        k = k + d_coeff*r_coeffs;
    end
end

normalize filter to 0 gain

F = F ./ k;

end % end of bilateral_base