SAMPLEDISK_BASE - Base function for SAMPLEDISK.

Syntax
Reference
See also
Function implementation
Subfunctions

Syntax

  [x, y, w] = SAMPLEDISK_BASE(center, radius, method, samp);

Reference

See discussions at http://mathworld.wolfram.com/DiskPointPicking.html http://mathworld.wolfram.com/GausssCircleProblem.html

Function implementation

%--------------------------------------------------------------------------
function [x, y, w] = sampledisk_base(center, radius, method, samp)

%error(nargchk(4, 5, nargin, 'struct'));
%error(nargoutchk(2, 3, nargout, 'struct'));

% set default
if nargout<=3,  w = [];  end

if any(strcmpi(method,{'full','grid','scale'}))
    radius = round(radius);
end

% % avoid duplicate entries calculations
% [radius, dum, J] = unique(radius);
% the sampling also depends on the variable samp, so unvalid approach

switch method
    case 'full' % sampling of all discrete points inside the circle
        [x, y, nsamp] = fullsampledisk(radius);

    case 'scale' % sampling of all discrete points inside the circle with
        % multiscale weight assignation
        [x, y, nsamp, w] = radisampledisk(radius);

    case 'grid' % regular grid sampling
        if samp>=0 && samp<1,
            n = floor(samp .* gausscircle(radius));
            samp = floor(4*radius/sqrt(n)); % our approximation
        end
        [x,y,nsamp] = gridsampledisk(radius, abs(samp));

    case 'radi' % radial sampling
        [x,y,nsamp] = radisampledisk1(radius, samp);

    case 'rand' % random sampling
        if all(samp(:)>=0) && all(samp(:)<1),
            samp = floor(samp .* gausscircle(radius));
        end
        [x,y,nsamp] = randsampledisk(radius, abs(samp));

    otherwise
        error('sampledisk_base:methoderror',['unknown method ' method]);

end

% % reset original ordering and set possible duplicate entries
% x = x(J,:);
% y = y(J,:);

% for i=1:length(x)
% x{i} = round(x{i} + repmat(center(i,1),[length(x{i}) 1]));
% y{i} = round(y{i} + repmat(center(i,2),[length(y{i}) 1]));
% end
x = round(x + repmat(center(:,1),[1 nsamp])); % rounds toward 0
y = round(y + repmat(center(:,2),[1 nsamp]));
% note that NaN number will still be NaN number after this operation.

if isempty(w),  w = ones(size(x));  end

end % end of sampledisk_base

Subfunctions

RADISAMPLEDISK - Sample on radial circles inside the disk

%--------------------------------------------------------------------------
function [x, y, nsamp, w] = radisampledisk(radius)
ndisks = length(radius);

% note: technique suggested in [DPG10]
% generate an adaptive grid around each center pixel so that samples are
% selected with increasing sparsity as the distance to the center (within
% the limit given by the radius) increases.
% reduce the grid resolution by two and compute on the coarser grid; repeat
% this process and continuously coarsen the grid; values from the fine grid
% are reused for the coarser grid so that there is no computational overhead.

% sampling rule
% the rate of sampling is fixed to 1/2 over all radial circles except for
% the first two circles with radius 1 and 2samp = repmat(0.5,[ndisks,1]);
%         irad:       1       2       3      4     5     6
%       radius:       1       2       4      8     16    32
%                  2^(i-1)    ...
%      no. pts:       4       8       8      16    32    64
%                  2^(i+1)  2^(i+1)  2^i    ...
% tot. no. pts:       5       13      21     37    69    133
%      (csamp)

rad = floor(log2(radius))+1;
rad(isinf(rad)) = 0;

R = max(radius);
Rad = floor(log2(R));

% list of considered radii
rsamp = 2.^(0:Rad);
% number of sample for each radius
nrsamp = 2*rsamp;
if Rad>=1,  nrsamp(1) = 4;
    if Rad>=2, nrsamp(2) = 8;  end
end
% cumulated number of samples
ncsamp = [0 cumsum(nrsamp,2)]+1;
% maximal number of samples
nsamp = ncsamp(end); % 1 stand for the added center of the circle

x = NaN(ndisks,nsamp);
y = NaN(ndisks,nsamp);

if nargout==4,
    w = zeros(ndisks,nsamp);
else
    w = [];
end

for i=1:Rad+1 % Rad+1 is length(rsamp)
    s = rand() * pi; % random pixel chosen chosen as the first sampling point
    theta = linspace(s,2*pi+s,nrsamp(i));
    rho = rsamp(i) * ones(1,nrsamp(i));
    [a,b] = pol2cart(theta, rho);
    I = rad>=i+1;
    nI = sum(I);
    x(I,ncsamp(i)+1:ncsamp(i+1)) = repmat(a,[nI,1]);
    y(I,ncsamp(i)+1:ncsamp(i+1)) = repmat(b,[nI,1]);
    if ~isempty(w) % multiscale weight factor
        w(I,ncsamp(i)+1:ncsamp(i+1)) = repmat(1/rsamp(i), [nI, nrsamp(i)]);
    end
end

% replace the first entry by the offset of the central point
x(:,1) = 0;
y(:,1) = 0;
if ~isempty(w),  w(:,1) = 1;  end
end

FULLSAMPLEDISK - Sample all lattice points inside a disk.

%--------------------------------------------------------------------------
function [x, y, nsamp, w] = fullsampledisk(radius)
% initialize
ndisks = length(radius);
R = max(radius);
nsamp = sum(sum(getnhood(strel('disk',R,0))));

if R>30
    warning('sampledisk:warningdata', ...
        ['large circles (max detected R=' num2str(R) ') imply too many ' ...
        'samples with method ''full'' and risk ''Out of Memory'' usage']);
end

x = NaN(nsamp,ndisks);
y = NaN(nsamp,ndisks);
% x = cell(ndisks,1);
% y = cell(ndisks,1);

if nargout==4,
    w = zeros(nsamp,ndisks);
    % r = cell(ndisks,1);
else
    w = [];
end

for i=1:ndisks
    offsets = getneighbors(strel('disk',radius(i),0));
    % when N equals 0, no approximation is used, and the structuring element
    % members consist of all pixels whose centers are no greater than R away
    % from the origin.
    k = size(offsets,1);
    x(1:k,i) = offsets(:,1);
    y(1:k,i) = offsets(:,2);
    % x{i} = offsets(:,1);
    % y{i} = offsets(:,2);
    if ~isempty(w) % multiscale weight factor
        % w(1:k,i) = 1 ./ floor(sqrt(offsets(:,1).^2 + offsets(:,2).^2));
        w(1:k,i) = 1 ./ sqrt(offsets(:,1).^2 + offsets(:,2).^2);
        % w{i} = 1 ./ sqrt(offsets(:,1).^2 + offsets(:,2).^2);
        % w{i}(isinf(r{i})) = 1;
    end
end

x = x';
y = y';
if ~isempty(w),  w(isinf(w)) = 1; w = w';   end
end

RANDSAMPLEDISK - Randomly sample inside a disk.

See http://mathworld.wolfram.com/DiskPointPicking.html

%--------------------------------------------------------------------------
function [x, y, nsamp] = randsampledisk(radius, samp)

ndisks = length(radius);
nsamp = max(samp);

if numel(samp)==1
    % probability density function (PDF) pdf_r(r)=(2/R^2) * r;
    % and cumulative PDF is F_r = (2/R^2)* (r^2)/2
    % inverse cumulative PDF is r = R*sqrt(F_r)
    % so we generate the correct r as
    rho = repmat(radius, [1 nsamp]) .* sqrt(rand(ndisks,nsamp));
    theta = 2 * pi * rand(ndisks,nsamp);
    % convert to cartesian
    [x,y] = pol2cart(theta, rho);

else   %if all(0<=samp && samp<1)
    x = NaN(ndisks,nsamp);
    y = NaN(ndisks,nsamp);
    for i=1:ndisks
        rho = repmat(radius(i), [1 samp(i)]) .* sqrt(rand(1,samp(i)));
        theta = 2 * pi * rand(1,samp(i));
        [x(i,1:samp(i)), y(i,1:samp(i))] = pol2cart(theta, rho);
    end
end
% at that point, samples are not unique
end

GRIDSAMPLEDISK - Sample inside the disk on a regular lattice grid.

%--------------------------------------------------------------------------
function [x, y, nsamp] = gridsampledisk(radius, samp)
% initialize
ndisks = length(radius);
if numel(samp)==1   % samp may be a scalar or a vector
    samp = repmat(samp,[ndisks,1]);
end

[~,i] = max(radius./ samp);
se = getnhood(strel('disk',radius(i),0));
% we look at the worse case
nsamp = sum(sum(se(1:samp(i):end,1:samp(i):end)))+1;
% note that we add 1 for the case the center of the circle (which is
% automatically added to sampling grid) is not already included in the
% grid
x = NaN(nsamp,ndisks);
y = NaN(nsamp,ndisks);

for i=1:ndisks
    se = getnhood(strel('disk',radius(i),0));
    grid = false(size(se));
    grid(1:samp(i):end,1:samp(i):end) = true;
    grid = grid & se;
    grid(radius(i)+1,radius(i)+1) = true;
    [m,n] = find(grid);
    k = size(m,1);
    x(1:k,i) = m - (radius(i)+1);
    y(1:k,i) = n - (radius(i)+1);
end

x = x';
y = y';
end

RADISAMPLEDISK1 - Sample on a single circle (at a distance radius from the disk's center)

%--------------------------------------------------------------------------
function [x, y, nsamp] = radisampledisk1(radius, samp)
ndisks = length(radius);

if numel(samp)==1   % samp may be a scalar or a vector
    samp = repmat(samp,[ndisks,1]);
end

r = radius;

I = samp>=1;
r(I) = min(radius(I), ceil(samp(I)/8));

I = samp<-1;
r(I) = ceil(radius(I)/2);
samp(I) = abs(samp(I));

I = samp>0 & samp<=1;
r(I) = ceil(samp(I) .* radius(I));
samp(I) = 8 * r(I);
samp((I) & radius==1) = 4;

nsamp = max(samp);

theta = NaN(ndisks,nsamp);
for i=1:ndisks
    theta(i,1:samp(i)) = linspace(0,2*pi,samp(i));
end

rho = r(:) * ones(1,nsamp);
[x,y] = pol2cart(theta, rho);
% replace the last (repeated) entry by the offset of the central point
x(:,end) = 0;
y(:,end) = 0;

end

GAUSSCIRCLE - Count the number of lattice points N inside the boundaries of a circle with radius r

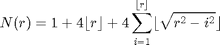
$N(r) = 1 + 4 \lfloor r \rfloor + 4 \sum_{i=1}^{\lfloor r\rfloor} \lfloor \sqrt{r^2 - i^2} \rfloor$

From http://mathworld.wolfram.com/GausssCircleProblem.html

%--------------------------------------------------------------------------
function N = gausscircle(r)
nr = size(r,1);
fr = floor(r);
frmax = max(fr);

R = repmat(r,[1 frmax]);
FR = meshgrid(1:frmax,1:nr);
FR = cumsum(floor(sqrt(R.^2 - FR.^2)),2);

N = 1 + 4*fr + 4*FR((fr-1)*nr+(1:nr)');
end

SAMPLEDISK_BASE - Base function for SAMPLEDISK.

Contents

Syntax

Reference

See also

Function implementation

Subfunctions