MUTUALSINGFRACTAL_BASE - Measure the mutual closeness of singularity spectra.
Contents
Description
Given two (possibly reduced) singularity spectra, quantify the degree of mutual closeness following the approach of [PTP09].
The mutual closeness of the multifractal spectra 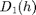 and
and 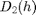 with
associated uncertainties
with
associated uncertainties  and
and 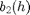 is
expressed by the Eq.(7) of [PTP09] as:
is
expressed by the Eq.(7) of [PTP09] as:
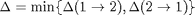
where:

and similarly for 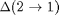 .
.
Syntax
delta = MUTUALSINGFRACTAL_BASE(h1, D1, b1, h2, D2, b2);
Inputs
h1, D1 : couple of estimation, ie the multifractal spectrum D1 of a (set of) signal(s) is estimated over a set of singularities h1.
b1 : associated uncertainty in the estimation.
h2, D2, b2 : ibid with an estimation performed over another (set of) signals.
Output
delta : mutual closeness.
Reference
[PTP09] O. Pont, A. Turiel, C.J. Perez-Vicente: "Empirical evidences of a common multifractal signature in economic, biological and physical systems", Physica A 388:3015-2035, 2009.
See also
Ressembles: FRACTALWAVE, FRACTALWAVESTAT. Requires: INTERP1, SUM, MIN.
Function implementation
function delta = mutualsingfractal_base(H1, DH1, ErrDH1, H2, DH2, ErrDH2)
first, define the directed weighted average difference: compute delta(1->2)
DH = interp1(H2, DH2, H1, 'linear'); ErrDH = interp1(H2, ErrDH2, H1, 'linear'); delta1 = sum(abs(DH1 - DH)./(ErrDH1.*ErrDH)) / sum(ErrDH1.*ErrDH);
compute delta(1->2)
DH = interp1(H1, DH1, H2, 'linear'); ErrDH = interp1(H1, ErrDH1, H2, 'linear'); delta = sum(abs(DH2 - DH)./(ErrDH2.*ErrDH)) / sum(ErrDH2.*ErrDH);
define the weighted average difference between the two reduced singularity spectra as the minimum of the two possible directed weighted average differences
delta = min(delta, delta1);
end % end of mutualsingfractal_base