GEODESICFILT_BASE - Base function for GEODESICFILT.

Contents

Syntax

   F = GEODESICFILT_BASE(I, method, iter, wei, winsize, a, ...
                       rho, sigma, der, int, samp, eign);

See also

Ressembles: GEODESICFILT, ADAPTIVEFILT_BASE, TENSANIFILT_BASE, TENSCALEDIRFILT_BASE, MDLFILT_BASE, CONVOLUTION_BASE, FMMISOPROPAGATION, FMMANISOPROPAGATION, FMM_BASE, PDEM. Requires: POTENTIAL2FRONT, IM2POTENTIAL, WEIGHTFILT_BASE.

Function implementation

function F = geodesicfilt_base(I, method, iter, wei, winsize, a, rho, sigma, ...
    der, int, samp, eign)

checking/setting parameters

% we also accept variable number of inputs
if nargin<=11
    eign = 'zen';
    if nargin<=10,
        samp = 1;
        if nargin<=9
            int = 'fast';
            if nargin<=8,  der = 'fast';  end
        end
    end
end

consider the iterative application of the algorithm

if iter>1
    F = I;
    for i=1:iter
        F = geodesicfilt_base(F, method, wei, winsize, rho, sigma, ...
            a, 1, der, int, samp, eign);
    end
    return
end

internal parameters

[X,Y,C] = size(I);

% the window of analysis: should be odd
winsize = round( (winsize-1)/2 )*2 + 1;
% center of the window
padnum = (winsize-1)/2;
% padnum = max([(winsize-1)/2 ceil(3*sigma) ceil(3*rho)])

% padd the original image for convenient processing
A = padarray(I,[padnum padnum],'replicate','both');

% create the output filtered image
F = zeros(size(I));

% over each local window, the value of the central pixel is estimated; it is
% also used as the starting point for local propagation
start_pt = [padnum+1;padnum+1];

compute once for all the potential function based on the gradient and/or the gradient structure tensor of the multispectral input image and define the propagation function: it is either a scalar field (isotropic case) providing with the speed (strenght) for the propagation (the higher the value at one point, the faster the propagation through this point) or a tensor field (anisotropic case) providing with a speed and a direction for the propagation.

T = im2potential(A, method, a, rho, sigma, der, int, samp, eign);

define the weighting function (see also function WEIGHTFILT_BASE)

if wei==0,     weighting = @wmedweight;
elseif wei>0,  weighting = @gaussweight;
else           weighting = @scaleweight;
end

perform local filtering: FMM is applied locally from the center of the window of analysis in orint to compute local distances from it; those distances are then weightened as to convolve the image locally; the final output value is assigned to the central pixel

estimation on local neighbourhoods

for jj = padnum+1:(padnum+X)
    for kk = padnum+1:(padnum+Y)
        xspan = jj-padnum:jj+padnum;
        yspan = kk-padnum:kk+padnum;

        % compute the matrix defining the metric: the geodesics will follow
        % regions where T is 'large'.
        Dwin = potential2front(T(xspan,yspan,:,:), start_pt);
        % Dwin = Dwin  /max(Dwin(:));

        for i=1:C
            Awin = A(xspan,yspan,i);
%             if i==1&&kk==20 &&jj==20
%                 figure,
%                 subplot(1,2,1), imagesc(rescale(Awin)), colormap gray, axis image
%                 subplot(1,2,2), imagesc(Dwin), colormap gray, axis image
%             end

            F(jj-padnum,kk-padnum,i) = weighting(Awin(:), Dwin(:), wei);
        end
    end

end

% % another way to do it: it uses the already implemented FMM_BASE function,
% % but implies many variable tests at each step of the loop
% for jj = padnum+1:(padnum+1+X-1)
%     for kk = padnum+1:(padnum+1+Y-1)
%         Dwin = fmm_base(T(jj-padnum:jj+padnum,kk-padnum:kk+padnum,:,:), ...
%             'sing', false, start_pt, [], O, [], Inf);
%         for i=1:C
%             Awin = A(jj-padnum:jj+padnum,kk-padnum:kk+padnum,i);
%             F(jj-padnum,kk-padnum,i) = weighting(Awin(:),Dwin(:),p);
%         end
%     end
%
% end

end % end of geodesicfilt_base

Subfunctions

GAUSSWEIGHT - Gaussian-based weighting function

%--------------------------------------------------------------------------
function k = gaussweight(Awin, Dwin, a)
Dwin = exp( - a * Dwin );
t = sum(Dwin);
if(t>0),    Dwin = Dwin/t;  end
k = sum(Awin.*Dwin);

end % end of gaussweight

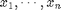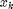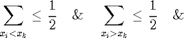
WMEDWEIGHT - Weighted median-based weighting function. For n numbers $x_1, \cdots, x_n$ with positive weights $w_1, \cdots, w_n$ (sum of all weights equal to one) the weighted median is defined as the element $x_k$, such that: $$ \sum_{x_i < x_k} \leq \frac{1}{2} \quad \& \quad \sum_{x_i > x_k} \leq \frac{1}{2} \quad \& \quad $$

%--------------------------------------------------------------------------
function k = wmedweight(Awin, Dwin)

Dwin = Dwin / max(Dwin(:));

% (line by line) transformation of the input-matrices to line-vectors
d = reshape(Awin',1,[]);
w = reshape(Dwin',1,[]);

% sort the vectors
A = [d' w'];
ASort = sortrows(A,1);

dSort = ASort(:,1)';
wSort = ASort(:,2)';

l = length(wSort);
sumVec = zeros(1,l);    % vector for cumulative sums of the weights
for i = 1:l
    sumVec(i) = sum(wSort(1:i));
end

k = [];     j = 0;

while isempty(k)
    j = j + 1;
    if sumVec(j) >= 0.5
        k = dSort(j);    % value of the weighted median
    end
end

end % end of wmedweight

SCALEWEIGHT - Scale-based weighting function.

%--------------------------------------------------------------------------
function k = scaleweight(Awin, Dwin, a)
Dwin = rescale(Dwin,eps,1) .^ a;
t = sum(Dwin);
if(t>0),    Dwin = Dwin/t;  end
k = sum(Awin.*Dwin);

end % end of scaleweight