MDLFILT_BASE - Base function for MDLFILT.

Contents

Syntax

   [depth,dl] = MDLFILT_BASE(I, scales, sm, der, rho, lam, ani);
   [depth,dl,best,scales] = MDLFILT_BASE(I, scales, sm, der, rho, lam, ani);

See also

Ressembles: MDLFILT, CONVOLUTION_BASE, ADAPTIVEFILT_BASE, GEODESICFILT_BASE, TENSANIFILT_BASE. Requires: GSTSMOOTH_BASE, SMOOTHFILT_BASE, TENSCALEDIRFILT_BASE, IMFILTER.

Function implementation

function [best_depth,dl,varargout] = mdlfilt_base(I, scales, sm, der, rho, lam, ani)

checking parameters and setting variable

[x y C] = size(I);

% if length(scales)==3 && scales(1)>scales(2)
%     scales = linspace(scales(2),scales(3),scales(1));
% end

treat the case where the range of scales was given as [step, min, max]

nscales = length(scales);

h = [0 1 0; 1 1 1; 0 1 0];

creating the description lenght matrix

dl = Inf * ones(x,y);

if nargout>=2
    varargout{1} = zeros(x,y);
    if nargout>=3,   varargout{2} = zeros(x,y);  end;
end

best_depth = zeros(size(I));

main computation

for i=1:nscales

creating a depth matrix

    if ani
        T = gstsmooth_base(I, rho, scales(i), der, sm, ...
            [], 1, false, false, 8, .4);
        [l1, l2, e1, e2] = gstdecomp(T);
        l1 = 1 ./ (sqrt(l1)+eps);
        l2 = 1 ./ (sqrt(l2)+eps);

        [gx2, gy2, gxy] = gstdecomp(l2,l1,e2,e1);

        T(:,:,1,1) = gx2;
        T(:,:,2,2) = gy2;
        T(:,:,1,2) = gxy;
        T(:,:,2,1) = T(:,:,1,2);
        depth = tenscaledirfilt_base(I, T, 1, [], [], 1, 12, 4, 0.5, false);
    else
        depth = smoothfilt_base(I, scales(i), sm, [], 1, [], [], []);
    end

estimating the residual

    residual = imfilter((I-depth).^2,h,'replicate');
    residual = sum(residual,3);
    % residual grows faster along the edges, that's the trick
    newdl = residual + lam/scales(i).^2;

find the minimal description: 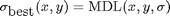$\sigma_{\mbox{best}}(x,y) = \mbox{MDL}(x,y,\sigma)$

    ir = newdl < dl;
    if ~isempty(ir)
        dl(ir) = newdl(ir);
        if nargout>=3
            % update the local optimal scale inside the scale map
            varargout{1}(ir) = i;
        end
        ir = repmat(ir,[1 1 C]);
        best_depth(ir) = depth(ir);
    end

end

if nargout==4,  varargout{2} = scales; end

end % end of mdlfilt_base