MDLFILT - Local adaptive filtering based on Minimal Description Length.

Description
Syntax
Inputs
Property [propertyname propertyvalues]
Outputs
Reference
See also
Function implementation

Description

Use Minimal Description Length principle to compute local adaptive neighborhoods and perform local filtering.

Local smoothness in term of variance: it estimates a local variance with the Minimal Description Length principle [Gomez00]. Coding two terms, the maximum smoothing and the minimal residual:

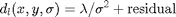
$d_l(x,y,\sigma) = \lambda/\sigma^2 + \mbox{residual}$

where 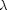$\lambda$ is (mainly) the assuming variance for the residual (it was modeled as a Gaussian density function).

Syntax

   dl = MDLFILT(I);
   [dl,depth,best,scales] = MDLFILT(I,scales);

Inputs

I : an input image with size (X,Y,C), where C>1 when I is multichannel.

scales : optional variable providing the range of scales used for local adaptive computation; it is:

either a 1D vector of lenght nsc giving the complete list of scales minsc:step:maxsc,
or a 1D vector of lenght 3 giving [nsc,minsc,maxsc] so that the range of scales will be calculated as linspace(minsc,maxsc,nsc);

default: scales=0.5:0.1:4.

Property [propertyname propertyvalues]

'int' : optional string setting the implementation used for estimating the gaussian derivatives:

'kro' for the (fast) 2D Gaussian smoothing with IMGAUSSIAN proposed by D.Kroon,
'pey' for the implementation 2D Gaussian filtering using the function PERFORM_CONVOLUTION as proposed by G.Peyre,
'mat' (or 'iso', default) for a direct implementation of the 2D smoothing using FSPECIAL and IMFILTER,

'lam' : lambda of the Minimal Description Length principle: mainly, the variance for the residual; default: lambda=3000.

Outputs

dl : image of description length.

depth : depth image.

best : image of local scale indexes: it gives for each the index of its scale in the vector scales, therefore the matrix scales(best) provides with the local scales.

scales : vector of scales used; when scales is passed, the same vector scales is output.

Reference

[Gomez00] G. Gomez: "Local smoothness in terms of variance", Proc. of BMVC, vol. 2, pp. 815:824, 2000. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.132.522

Function implementation

function [dl,varargout] = mdlfilt(I,varargin)

parsing and checking parameters

if ~(isnumeric(I))
    error('mdlfilt:inputerror','a matrix is required in input');
end

error(nargchk(1, 8, nargin, 'struct'));
error(nargoutchk(1, 4, nargout, 'struct'));

p = createParser('MDLFILT');
% optional parameters
p.addOptional('scales',0.5:0.1:4, @(x)isempty(x) || ...
    (nb_dims(x)==1 && length(x)>=2));
p.addParamValue('int', 'fast', @(x)ischar(x) && ...
    any(strcmpi(x,{'fast','matlab','conv','ani'})));
p.addParamValue('lam', 3000, @(x)isscalar(x) && x<=3000 && x>=0);

p.addParamValue('ani', false, @(x)islogical(x));
p.addParamValue('rho', 3, @(x)isscalar(x) && isfloat(x) && x>=0);
p.addParamValue('der', 'pey', @(x)ischar(x) && ...
    any(strcmpi(x,{'mat','prew','sob','pey','kro'})));

% parse and validate all input arguments
p.parse(varargin{:});
p = getvarParser(p);

checking parameters and setting variable

if nargin>=2 && isempty(p.scales) % reset to the default
    p.scales = 0.5:0.1:4;
end

% treat the case where the range of scales was given as [step, min, max]
if length(p.scales)==3 && p.scales(1)>p.scales(2)
    p.scales = linspace(p.scales(2),p.scales(3),p.scales(1));
end

main calculation

[depth,dl,best,p.scales] = mdlfilt_base(I, p.scales, p.int, p.der, p.rho, p.lam, p.ani);

if nargout>=3
    varargout{1} = best;
    if nargout==4,  varargout{2} = p.scales;  end;
end

display

if p.disp
    figure, subplot(1,2,1),
    imshow(rescale(depth,0,1)), axis image off; title('MDL filtered image');
    subplot(1,2,2),
    imshow(rescale(dl,0,1)), axis image off; title('description length');
end

end % end of mdlfilt